Продуктивність оптимізації на синтетичних гаусових та деревоподібних вбудовуваннях

Таблиця посилань

Анотація та 1. Вступ

1. Пов'язані роботи

2. Техніки опуклої релаксації для гіперболічних SVM

   3.1 Попередні відомості

   3.2 Оригінальна формулювання HSVM

   3.3 Напіввизначена формулювання

   3.4 Момент-сума-квадратів релаксація

3. Експерименти

   4.1 Синтетичний набір даних

   4.2 Реальний набір даних

4. Обговорення, подяки та посилання

   \

A. Докази

B. Вилучення розв'язку в послабленій формулювації

C. Про ієрархію релаксації момент-сума-квадратів

D. Масштабування Платта [31]

E. Детальні результати експериментів

F. Робастна гіперболічна машина опорних векторів

4.1 Синтетичний набір даних

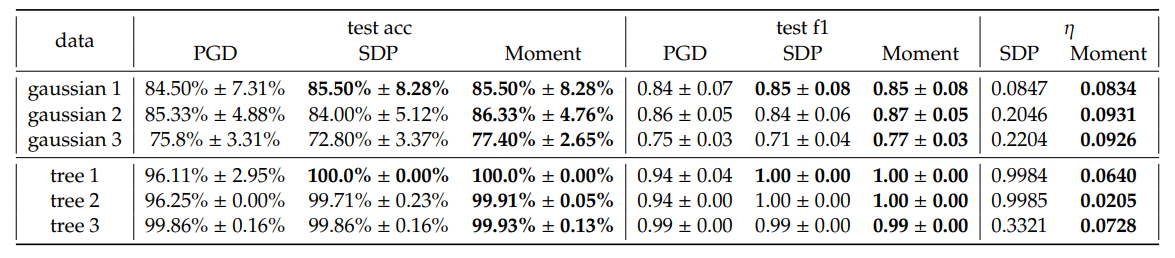
\ Загалом, ми спостерігаємо невелике покращення середньої точності тесту та зваженого F1 показника від SDP і Moment відносно PGD. Примітно, що ми спостерігаємо, що Moment часто показує більш послідовні покращення порівняно з SDP у більшості конфігурацій. Крім того, Moment дає менші оптимальні проміжки 𝜂, ніж SDP. Це відповідає нашим очікуванням, що Moment є щільнішим, ніж SDP.

\ Хоча в деяких випадках, наприклад, коли 𝐾 = 5, Moment досягає значно менших втрат порівняно як з PGD, так і з SDP, це, як правило, не так. Ми підкреслюємо, що ці втрати не є прямими вимірюваннями узагальнюваності гіперболічних роздільників з максимальним відступом; швидше, вони є комбінаціями максимізації відступу та штрафу за неправильну класифікацію, що масштабується з 𝐶. Отже, спостереження, що продуктивність точності тесту та зваженого F1 показника є кращою, хоча втрати, обчислені з використанням вилучених розв'язків з SDP і Moment, іноді вищі, ніж від PGD, може бути пов'язане зі складним ландшафтом втрат. Більш конкретно, спостережувані збільшення втрат можна пояснити складністю ландшафту, а не ефективністю методів оптимізації. На основі результатів точності та F1 показника, емпірично методи SDP і Moment виявляють розв'язки, які краще узагальнюються, ніж ті, що отримані лише запуском градієнтного спуску. Ми надаємо більш детальний аналіз впливу гіперпараметрів у додатку E.2 та час виконання в таблиці 4. Межа рішення для Gaussian 1 візуалізована на рисунку 5.

\

\ Синтетичне вкладення дерева. Оскільки гіперболічні простори добре підходять для вкладення дерев, ми генеруємо випадкові графи дерев і вкладаємо їх у H2, слідуючи Mishne et al. [6]. Зокрема, ми позначаємо вузли як позитивні, якщо вони є дочірніми для вказаного вузла, і негативні в іншому випадку. Потім наші моделі оцінюються для класифікації піддерев, з метою визначення межі, яка включає всі дочірні вузли в межах одного піддерева. Таке завдання має різні практичні застосування. Наприклад, якщо дерево представляє набір токенів, межа рішення може виділити семантичні області в гіперболічному просторі, які відповідають піддеревам графа даних. Ми підкреслюємо, що загальною особливістю такого завдання класифікації піддерев є дисбаланс даних, який зазвичай призводить до поганої узагальнюваності. Отже, ми прагнемо використовувати це завдання для оцінки продуктивності наших методів у цих складних умовах. Три вкладення обрані та візуалізовані на рисунку 3, а продуктивність узагальнена в таблиці 1. Час виконання обраних дерев можна знайти в таблиці 4. Межа рішення дерева 2 візуалізована на рисунку 6.

\ Подібно до результатів синтетичних наборів даних Гаусса, ми спостерігаємо кращу продуктивність від SDP і Moment порівняно з PGD, і через дисбаланс даних, з яким методи GD зазвичай мають труднощі, ми маємо більший приріст у зваженому F1 показнику в цьому випадку. Крім того, ми спостерігаємо великі оптимальні проміжки для SDP, але дуже щільний проміжок для Moment, що підтверджує оптимальність Moment навіть коли дисбаланс класів є серйозним.

\

\

:::info Автори:

(1) Sheng Yang, John A. Paulson School of Engineering and Applied Sciences, Harvard University, Cambridge, MA (shengyang@g.harvard.edu);

(2) Peihan Liu, John A. Paulson School of Engineering and Applied Sciences, Harvard University, Cambridge, MA (peihanliu@fas.harvard.edu);

(3) Cengiz Pehlevan, John A. Paulson School of Engineering and Applied Sciences, Harvard University, Cambridge, MA, Center for Brain Science, Harvard University, Cambridge, MA, and Kempner Institute for the Study of Natural and Artificial Intelligence, Harvard University, Cambridge, MA (cpehlevan@seas.harvard.edu).

:::

:::info Ця стаття доступна на arxiv за ліцензією CC by-SA 4.0 Deed (Attribution-Sharealike 4.0 International).

:::

\