Wydajność optymalizacji na syntetycznych osadzeniach gaussowskich i drzewiastych

Spis odnośników

Streszczenie i 1. Wprowadzenie

1. Prace powiązane

2. Techniki wypukłej relaksacji dla hiperbolicznych SVM

   3.1 Wstęp

   3.2 Oryginalna formulacja HSVM

   3.3 Formulacja półokreślona

   3.4 Relaksacja momentowo-sumo-kwadratowa

3. Eksperymenty

   4.1 Zbiór danych syntetycznych

   4.2 Rzeczywisty zbiór danych

4. Dyskusje, Podziękowania i Bibliografia

   \

A. Dowody

B. Ekstrakcja rozwiązań w sformułowaniu zrelaksowanym

C. O hierarchii relaksacji momentowo-sumo-kwadratowej

D. Skalowanie Platta [31]

E. Szczegółowe wyniki eksperymentów

F. Odporny hiperboliczny Support Vector Machine

4.1 Zbiór danych syntetycznych

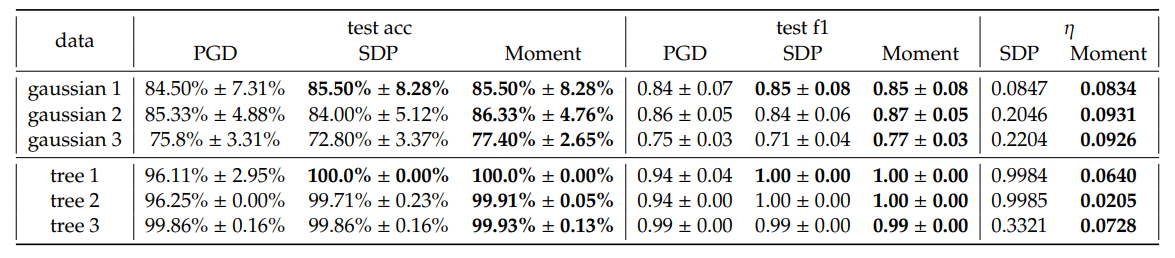
\ Ogólnie rzecz biorąc, obserwujemy niewielki wzrost średniej dokładności testowej i ważonego wyniku F1 dla SDP i Moment w porównaniu do PGD. Warto zauważyć, że Moment często wykazuje bardziej spójne poprawy w porównaniu z SDP, w większości konfiguracji. Ponadto Moment daje mniejsze luki optymalności 𝜂 niż SDP. Jest to zgodne z naszym oczekiwaniem, że Moment jest bardziej precyzyjny niż SDP.

\ Chociaż w niektórych przypadkach, na przykład gdy 𝐾 = 5, Moment osiąga znacznie mniejsze straty w porównaniu zarówno z PGD, jak i SDP, generalnie nie jest to reguła. Podkreślamy, że te straty nie są bezpośrednimi pomiarami zdolności do generalizacji hiperbolicznych separatorów maksymalnego marginesu; są raczej kombinacją maksymalizacji marginesu i penalizacji za błędną klasyfikację, która skaluje się z 𝐶. Stąd obserwacja, że wydajność w zakresie dokładności testowej i ważonego wyniku F1 jest lepsza, mimo że strata obliczona przy użyciu rozwiązań wyekstrahowanych z SDP i Moment jest czasami wyższa niż ta z PGD, może wynikać ze skomplikowanego krajobrazu strat. Dokładniej rzecz ujmując, obserwowane wzrosty strat można przypisać zawiłościom krajobrazu, a nie skuteczności metod optymalizacji. Na podstawie wyników dokładności i wyniku F1, empirycznie metody SDP i Moment identyfikują rozwiązania, które lepiej się generalizują niż te uzyskane wyłącznie poprzez uruchomienie spadku gradientu. Szczegółową analizę wpływu hiperparametrów przedstawiamy w Dodatku E.2, a czas wykonania w Tabeli 4. Granica decyzyjna dla Gaussiana 1 jest zwizualizowana na Rysunku 5.

\

\ Syntetyczne osadzenie drzewa. Ponieważ przestrzenie hiperboliczne są dobre do osadzania drzew, generujemy losowe grafy drzew i osadzamy je w H2, postępując zgodnie z Mishne i in. [6]. W szczególności oznaczamy węzły jako pozytywne, jeśli są dziećmi określonego węzła, a w przeciwnym razie jako negatywne. Nasze modele są następnie oceniane pod kątem klasyfikacji poddrzew, mając na celu identyfikację granicy, która obejmuje wszystkie węzły potomne w obrębie tego samego poddrzewa. Takie zadanie ma różne praktyczne zastosowania. Na przykład, jeśli drzewo reprezentuje zbiór tokenów, granica decyzyjna może podkreślać regiony semantyczne w przestrzeni hiperbolicznej, które odpowiadają poddrzewom grafu danych. Podkreślamy, że powszechną cechą takiego zadania klasyfikacji poddrzew jest brak równowagi danych, który zwykle prowadzi do słabej zdolności do generalizacji. Dlatego staramy się wykorzystać to zadanie do oceny wydajności naszych metod w tych trudnych warunkach. Wybrano trzy osadzenia i zwizualizowano je na Rysunku 3, a wydajność podsumowano w Tabeli 1. Czas wykonania wybranych drzew można znaleźć w Tabeli 4. Granica decyzyjna drzewa 2 jest zwizualizowana na Rysunku 6.

\ Podobnie jak w wynikach syntetycznych zbiorów danych Gaussa, obserwujemy lepszą wydajność SDP i Moment w porównaniu z PGD, a ze względu na brak równowagi danych, z którym metody GD zazwyczaj mają problemy, mamy większy wzrost ważonego wyniku F1 w tym przypadku. Ponadto obserwujemy duże luki optymalności dla SDP, ale bardzo wąską lukę dla Moment, potwierdzając optymalność Moment nawet wtedy, gdy brak równowagi klas jest poważny.

\

\

:::info Autorzy:

(1) Sheng Yang, John A. Paulson School of Engineering and Applied Sciences, Harvard University, Cambridge, MA (shengyang@g.harvard.edu);

(2) Peihan Liu, John A. Paulson School of Engineering and Applied Sciences, Harvard University, Cambridge, MA (peihanliu@fas.harvard.edu);

(3) Cengiz Pehlevan, John A. Paulson School of Engineering and Applied Sciences, Harvard University, Cambridge, MA, Center for Brain Science, Harvard University, Cambridge, MA, oraz Kempner Institute for the Study of Natural and Artificial Intelligence, Harvard University, Cambridge, MA (cpehlevan@seas.harvard.edu).

:::

:::info Niniejszy artykuł jest dostępny na arxiv na licencji CC by-SA 4.0 Deed (Attribution-Sharealike 4.0 International).

:::

\