Non-Fermi Liquids: Diverse NFL Scaling Behaviors
Table of Links
- Prologue
- Diagrammatic(s) Rules
- Straight-forward Eikonal
- Legacy Bosonization
- Wonton Holography
- Holographic Propagators
- Strange Cuprates
- Stranger Things
- Epilogue
Stranger Things
\ The propagator (21) obtained with the use of (44) was shown to develop three distinct FS [44], thus hinting at flattening of the renormalized fermion dispersion and bringing about an intrinsic instability towards the formation of a ’flat band’ characterized by z > 1 [20, 45].
\ Interestingly, if the interaction function D(ω, k) were to be molded into (1) by choosing ρ = 2 and ξ → −∞ the HV exponents would be taking values z = 1, θ = 0, thus satisfying (41) but not (40). On the other hand, matching the holographic asymptotics (31) would only be possible for θ = 2 which doesn’t satisfy (40) either.
\ The interactions (1) with ξ = ρ = 1 also arise in the 2d problem of half-filled Landau level with unscreened Coulomb interactions [5]. The first-order self-energy (4) now demonstrates a ’marginal FL’ behavior
\ 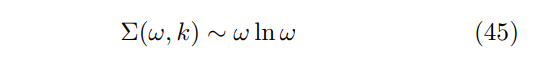
\ In the N → 0 limit one then obtains the counterpart of (11)
\ 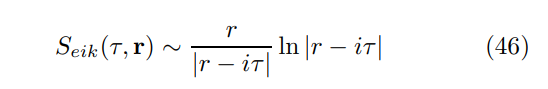
\ which would be marginally consistent - as far as the overall power-counting is concerned - with the holographic action (31) that would yield mere constants (or, at most, logarithms) for z = 1 and θ = 0 in both large-r and -τ limits.
\ Similar to the discussion of the case ξ = 1, it has been argued that the behavior (46) can only develop in some intermediate regime. By contrast, at the longest times an essentially free algebraic behavior, G(τ, r → 0) ≈ G0(τ, r → 0), was found, whereas at large distances the propagator was predicted to experience no more than a logarithmic suppression, G(τ → 0, r) ≈ G0(τ → 0, r)/ ln r [8].
\ 
\ Yet another physically relevant example of the 2d interaction (1) with ρ = 2, ξ = 0 corresponds to the socalled ’spin-fermion’ model of itinerant fermions coupled by antiferromagnetic fluctuations where the momentum k is measured with respect to the AFM ordering vector [46]. Neglecting the (in fact, all-important) complications associated with a non-circular shape of the realistic FS one computes (10) in the form
\ 
\ Also, the theory of compressible even-denominator QHE states that were originally described in terms of the finite density ’composite fermions’ [5], was later reformulated to elucidate its hidden Dirac properties [47, 48].
\ In 1d the pseudo-relativistic behavior sets in generically in the presence of partially filled bands. By using the standard bosonization one readily obtains the faster-than-algebraic decay of the propagator [49]
\ 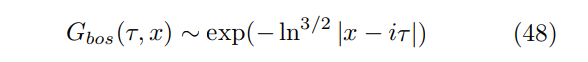
\ that can be thought of as the 1d analog of the Mott insulating state. Considering that in 1d no Landau damping can occur, the formal values of the HV exponents, z = 1 and θ = 0, obtained from (4) and (41) for ρ = 0 and ξ → −∞ yield the asymptotics (31) whose power counting is roughly consistent with (48).
\ 
\ Contrary to the original expectations, though, the amplitude (49) was shown to manifest η3 < 0 under the use of a gauge invariance-preserving regularization scheme [51].
\ Obviously, being just one (albeit a rather natural one) out of infinitely many other gauge-invariant amplitudes the function (49) may not be necessarily representative of the general behavior. In fact, its dependence on the contour Γ is somewhat reminiscent of that on the gauge in the case of the ordinary (non-gauge-invariant, albeit unique) propagator.
\ 
\
:::info Author:
(1) D. V. Khveshchenko, Department of Physics and Astronomy, University of North Carolina, Chapel Hill, NC 27599.
:::
:::info This paper is available on arxiv under CC BY 4.0 DEED license.
:::
\
You May Also Like

BounceBit plans to use platform fees for BB repurchase
Best Crypto to Buy Now: Can DeepSnitch AI Do 100x in 2025?
