Beyond Cycles of Deviation: How Fair Principles Ensure a Stable Nash Equilibrium
Table of Links
Abstract and 1. Introduction
-
A free and fair economy: definition, existence and uniqueness
2.1 A free economy
2.2 A free and fair economy
-
Equilibrium existence in a free and fair economy
3.1 A free and fair economy as a strategic form game
3.2 Existence of an equilibrium
-
Equilibrium efficiency in a free and fair economy
-
A free economy with social justice and inclusion
5.1 Equilibrium existence and efficiency in a free economy with social justice
5.2 Choosing a reference point to achieve equilibrium efficiency
-
Some applications
6.1 Teamwork: surplus distribution in a firm
6.2 Contagion and self-enforcing lockdown in a networked economy
6.3 Bias in academic publishing
6.4 Exchange economies
-
Contributions to the closely related literature
-
Conclusion and References
Appendix
3.2 Existence of an equilibrium
In this section, we state and prove our main result.
\ 
\ 
\ 
\ 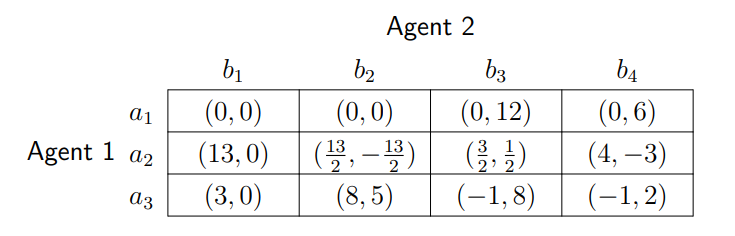
\ In the strategic form game in Table 4, the sum of excess payoffs in any cycle of outcomes equals 0. Therefore, the game does not admit a cycle of deviations. The profile x ∗ = (a2, b3) is the only pure strategy Nash equilibrium of the game.
\ Note that the game in Table 4 is generated from a free and fair economy. From Definition 7, a sufficient condition for a finite strategic form game to admit a pure strategy Nash equilibrium is the absence of a cycle of deviations. The sum of excess payoffs in any cycle of deviations has to be strictly positive, as illustrated in Table 3 in Example 2. Such an example of a cycle of deviations can not be constructed in a strategic form game generated from a free and fair economy (see Table 4 in Example 2). We prove that in a strategic form game generated by a free and fair economy, the sum of excess payoffs in any cycle of deviations equals 0.
\ 
\ 
\ The principles of market justice that define a free and fair economy are only sufficient conditions for the existence of a pure strategy Nash equilibrium. However, an economy that violates the fair principles may not have a pure strategy Nash equilibrium.
\
:::info Authors:
(1) Ghislain H. Demeze-Jouatsa, Center for Mathematical Economics, University of Bielefeld (demeze jouatsa@uni-bielefeld.de);
(2) Roland Pongou, Department of Economics, University of Ottawa (rpongou@uottawa.ca);
(3) Jean-Baptiste Tondji, Department of Economics and Finance, The University of Texas Rio Grande Valley (jeanbaptiste.tondji@utrgv.edu).
:::
:::info This paper is available on arxiv under CC BY 4.0 DEED license.
:::
\
You May Also Like

Tether to Launch USAT Stablecoin in the United States

Best Altcoins to Buy Now – Crypto Expert’s Top Picks For September 2025
